COLUMN
MATLAB®とC言語による開発の比較 - それぞれの言語を開発において
有効活用する方法① -
2019.07.31
システム開発では、C言語に加えてMATLAB®などのシミュレーション言語を利用する機会が増えてきています。開発を効率よく行うためには、C言語とMATLAB®のどちらの方法が適切でしょうか。それは、開発ターゲットや開発事象により異なるので、それぞれの言語の特長を把握して、どの方法が適切であるかの判断が必要です。
本コラムでは、制御工学や通信工学、画像処理などで広く用いられているフィルタを例題に、C言語とMATLAB®による開発の比較を行います。フィルタ設計に関しては、予備知識が必要ないように基礎から説明します。フィルタ設計から検証までの各プロセスにおいて、C言語とMATLAB®を使用したときの特長について解説します。
1.フィルタとは
フィルタという言葉で皆さんは何を連想するでしょうか。コーヒーのフィルタや空気清浄機のフィルタなどを連想されるのではないでしょうか。では、これらのフィルタに共通することは何でしょうか。それは不要なものを取り除くという働きです。コーヒーかすや、空気中のゴミや花粉を取り除くために用いられるものがフィルタです。
私たちの身の回りのエレクトロニクス製品でも、見えないところで電気的なフィルタがよく用いられています。たとえば、TVではチャンネルを選択すると、選択した放送局以外の不要な信号をフィルタで取り除くことで、見たいチャンネルの映像を見ることができます。またオーディオ製品では、信号処理の過程で発生した雑音をフィルタで取り除くことでクリアなサウンドを再生しています。スマートフォンの電源でも電圧変動を抑えるためにフィルタが使われています。フィルタが使われていないエレクトロニクス製品はほとんどないといってよいでしょう。
コーヒーや空気清浄機のフィルタでは、不要な物質の大きさよりも小さな隙間の繊維を用いることで不要な物質を取り除いています。では、電気的なフィルタでは、どうやって不要な信号を取り除いているのでしょうか。信号にはさまざまな周波数成分が含まれており、電気的なフィルタでは、この周波数を利用して不要な信号を取り除いています。周波数というのは1秒間に繰り返される波の数のことで、単位はHzを用います。具体例を用いて以下で説明します。
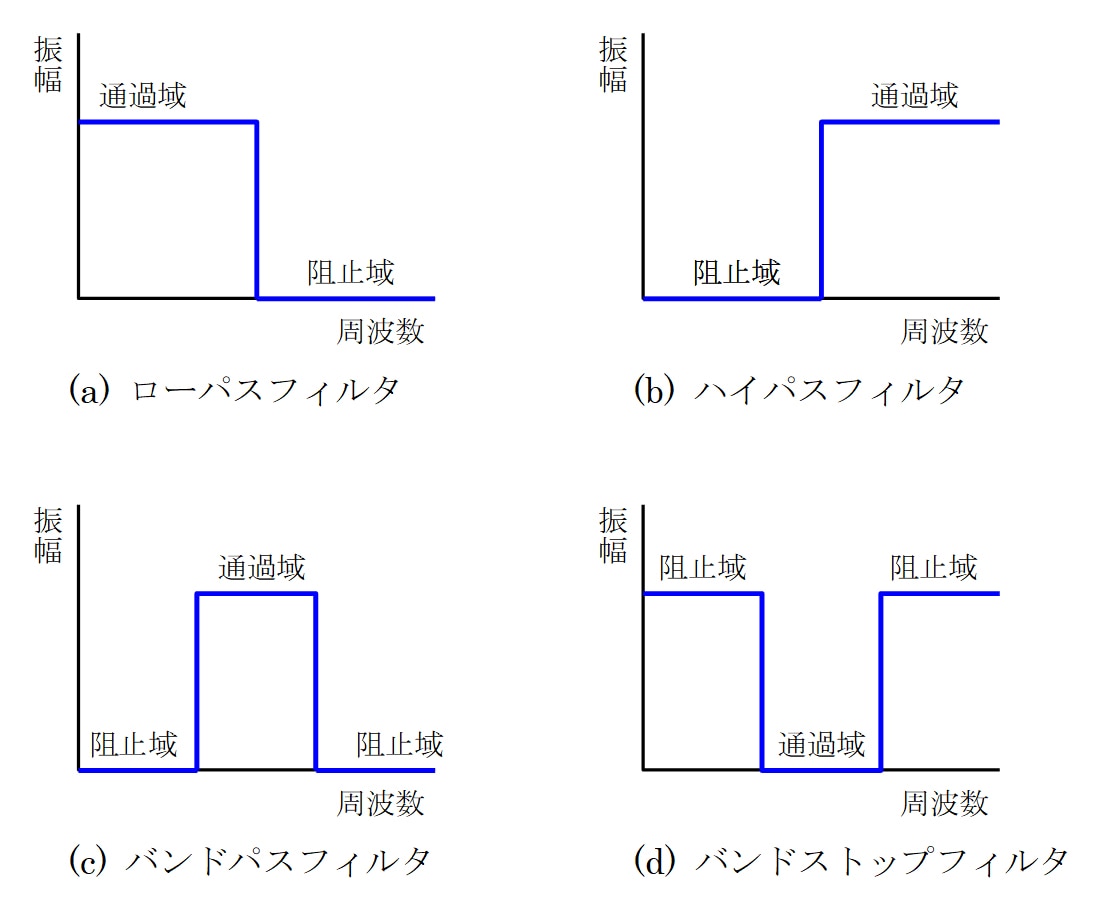
Fig.1 フィルタの種類
音声信号の主要な周波数成分は300~3.4kHzに分布していることが知られています。音声に300~10kHzの周波数範囲で均一に雑音が加わっている場合、3.4kHz以上の周波数成分を取り除くフィルタを用いることで3.4kHz以上の雑音が除去されて、よりクリアにその音声を聞くことができるようになります。電気的なフィルタには、この例のようにある周波数以上の成分を取り除くフィルタ(Fig.1(a)のローパスフィルタ)のほかに、Fig.1に示されるようにさまざまな特性のフィルタがあります。
2. MATLAB®とC言語による開発の比較
Fig.1(a)の振幅特性を持つローパスフィルタを設計するプログラムをC言語とMATLAB®で作成し、プログラムのコード効率や速度の比較などを行うことで、それぞれの言語の特長について述べていきます。わかりやすい例題として、フィルタ設計法の中で最も簡単な式で表される、バタワースフィルタと呼ばれる設計法を用います。
2.1 バタワースフィルタの振幅特性の理論式
バタワースフィルタの振幅特性は下記の式で与えられます。
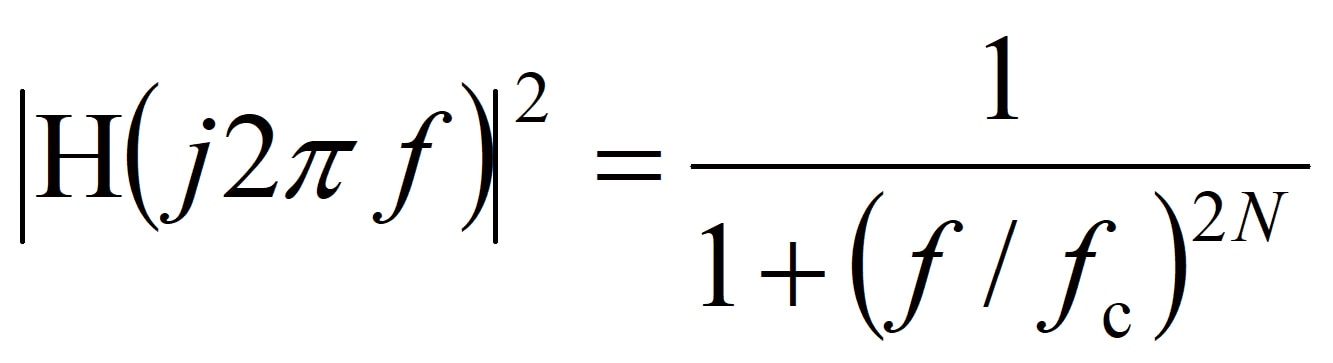
(1)
ただし、j 虚数単位、N はフィルタ次数、fcは定数のカットオフ周波数、f は変数の周波数です。
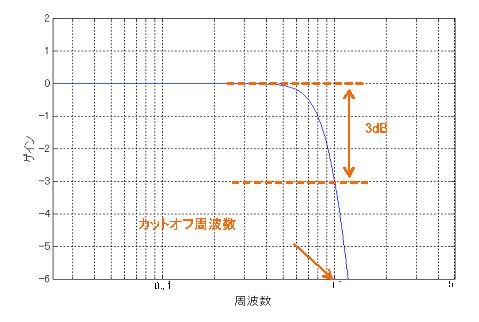
Fig.2 バタワースフィルタの振幅特性
Fig.2 は、カットオフ周波数 を1にして、周波数 を0Hzから5Hzまで変化させたときの式(1)の値を対数でプロットしたものです。この図から、前述のローパスフィルタの特性となっていることがわかります。f がカットオフ周波数と同じ値1のとき、式(1)の値は(デシベルで表すと3dB※)となります。このようにカットオフ周波数とは振幅特性が3dB減衰する周波数のことを指します。
※
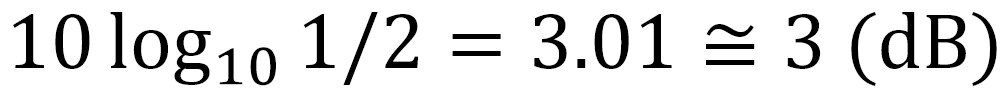
2.2 極の導出
フィルタ設計は、式(1)で与えられる振幅特性を持つフィルタの伝達関数を求めることです。この伝達関数を求めるために必要になるのが、極と呼ばれるものです。式(1)はラプラス演算子S を用いて表すと以下のように書き直すことができます。
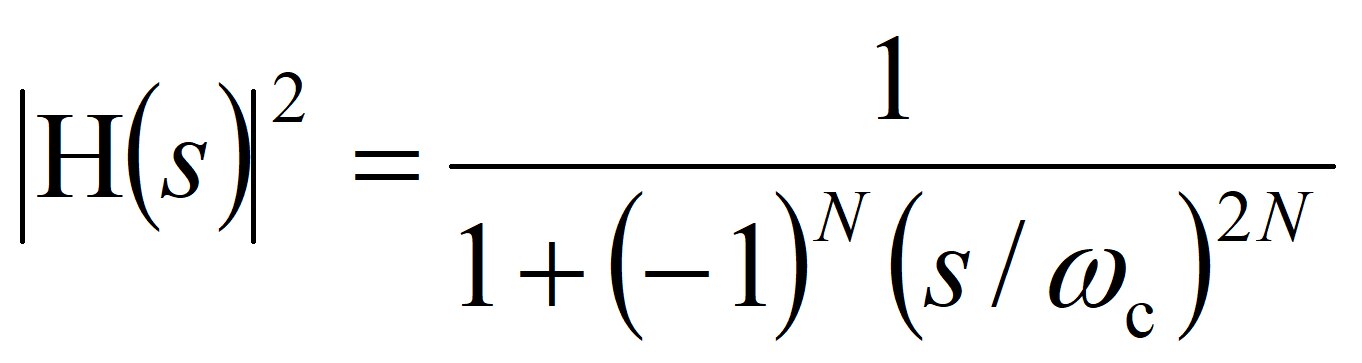
(2)
ただし、 s = jω = j2πf、 ωc = 2πfcです。 ωを角周波数、 ωc をカットオフ角周波数といいます。
式(2)は複素関数 の2乗となっていますので、ある関数とその関数の共役を掛けたときに、この式の右辺になるような、ある関数がバタワースフィルタの伝達関数となります。分子は1なので、分母の関数がわかればフィルタの伝達関数が求まります。
以下では、簡単化のために ωc = 1として、Nが1と2のとき分母の関数がどのようになるのかについて考えていきます。
①N = 1のとき
式(2)の分母は1 ー s2となり、s2 = 1を満たす2つの根α, βを求めて1 ー s2 = ー(s-α)(s ー β)と展開したときのs-αかs ー βがバタワースフィルタの分母の関数になります。この根α, βのことをフィルタの極といいます。
ここでは、式(2)の分母の項(-1)Nが-1になるNが1以上の奇数のときにも同じ考え方で一般解となるように、極α, βをオイラーの公式を用いて求めていきます。
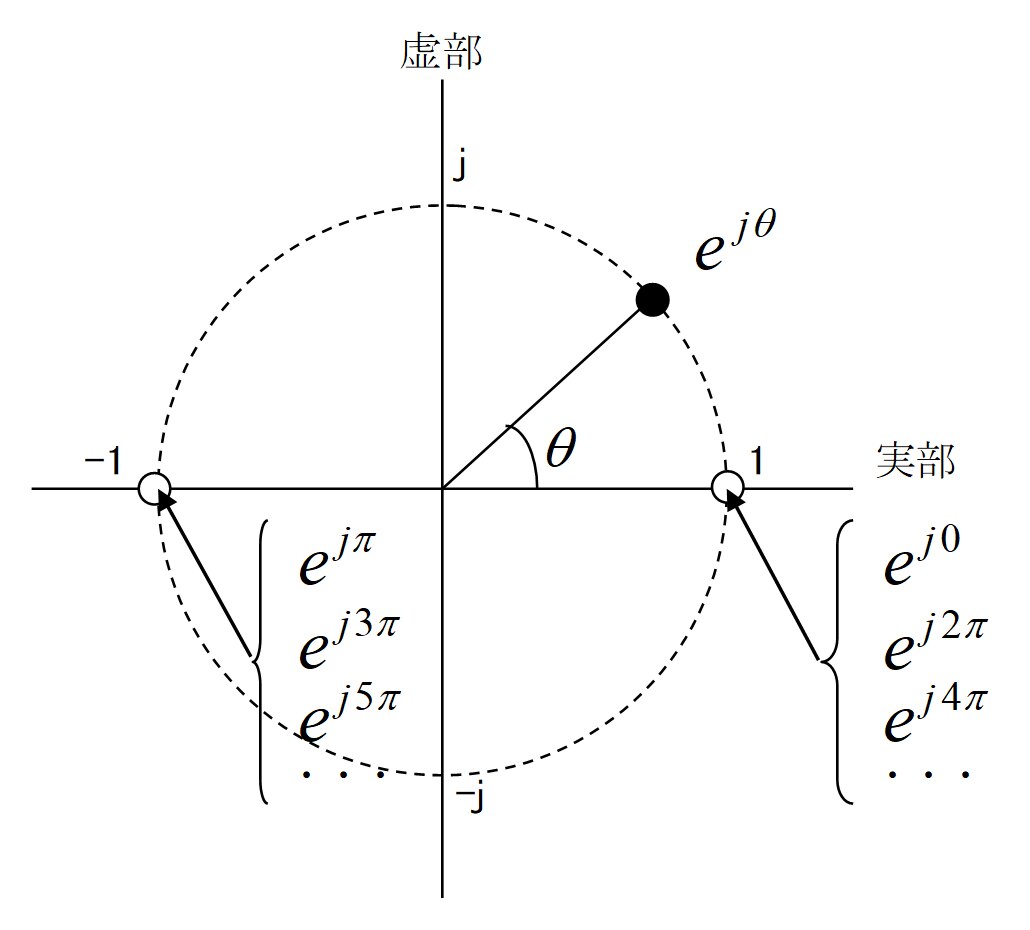
Fig.3 オイラーの公式の幾何学的表示
オイラーの公式
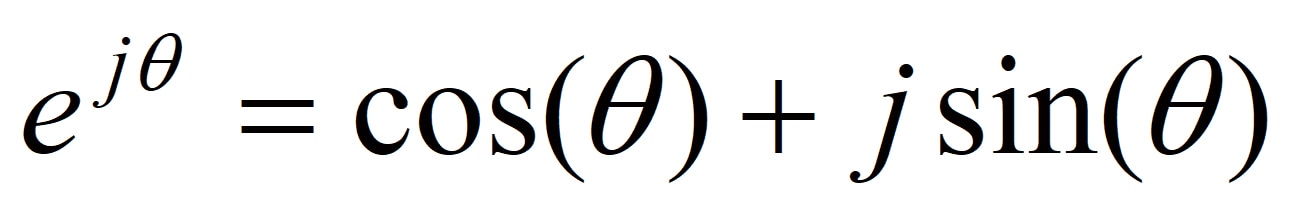
(3)
を用いると、Fig.3に示されるように1という数字はej2πk(kは整数)と表すことができます。
よって極は、s2 = 1 ⇒ s2 = ej2πkを解くことで
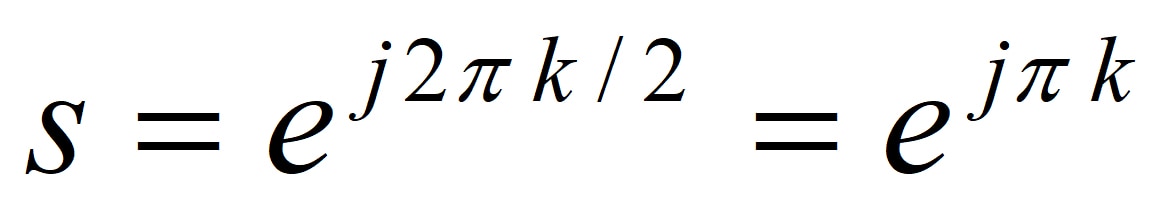
(4)
から±1と求まります。
従って、1 ー s2 = (s + 1)(s ー 1 )と展開できますので、s + 1もしくはs ー 1のどちらか一方がバタワースフィルタの伝達関数の分母となります。どちらを選ぶべきかについては後述します。
②N = 2のとき
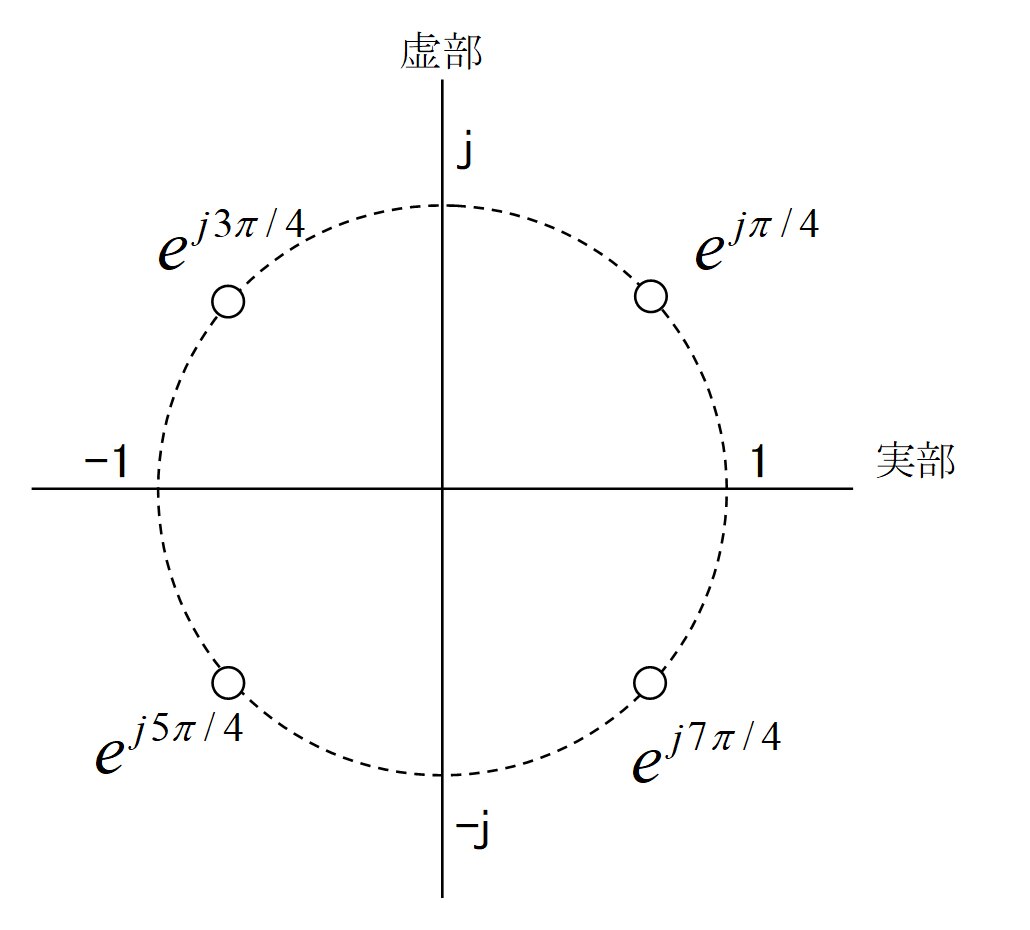
Fig.4 N = 2のときの極配置
式(2)の分母はとなるので、極はを解くことで
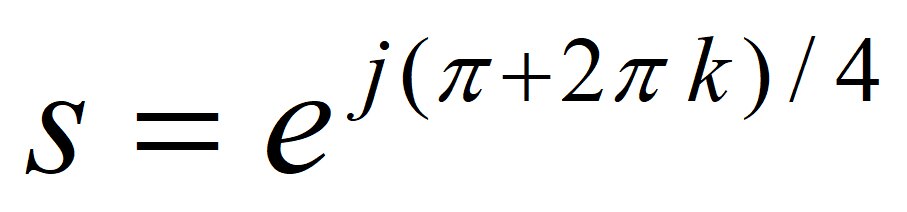
(5)
となり、Fig.4の丸印で示されるように極は円周上に等間隔に分布します。
従って、 s ー ejπ/4 , s ー ej3π/4 , s ー ej5π/4 , s ー ej7π/4 の4つの関数の中から2つの関数を選んで、それらを掛けたものがバタワースフィルタの伝達関数の分母になります。残りの2つの関数を掛けたものが、この関数の共役関数になります。
上記では簡単化のためにとしていましたが、任意の ωc に対する極 pk は、式(4)、(5)から次式のようになります。
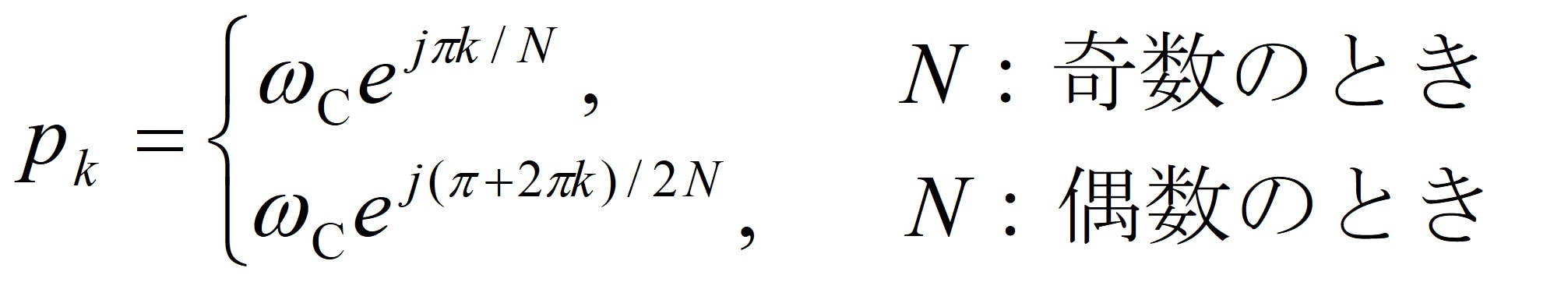
(6)
ただし、 k = 0,1,2,...2Nー1です。
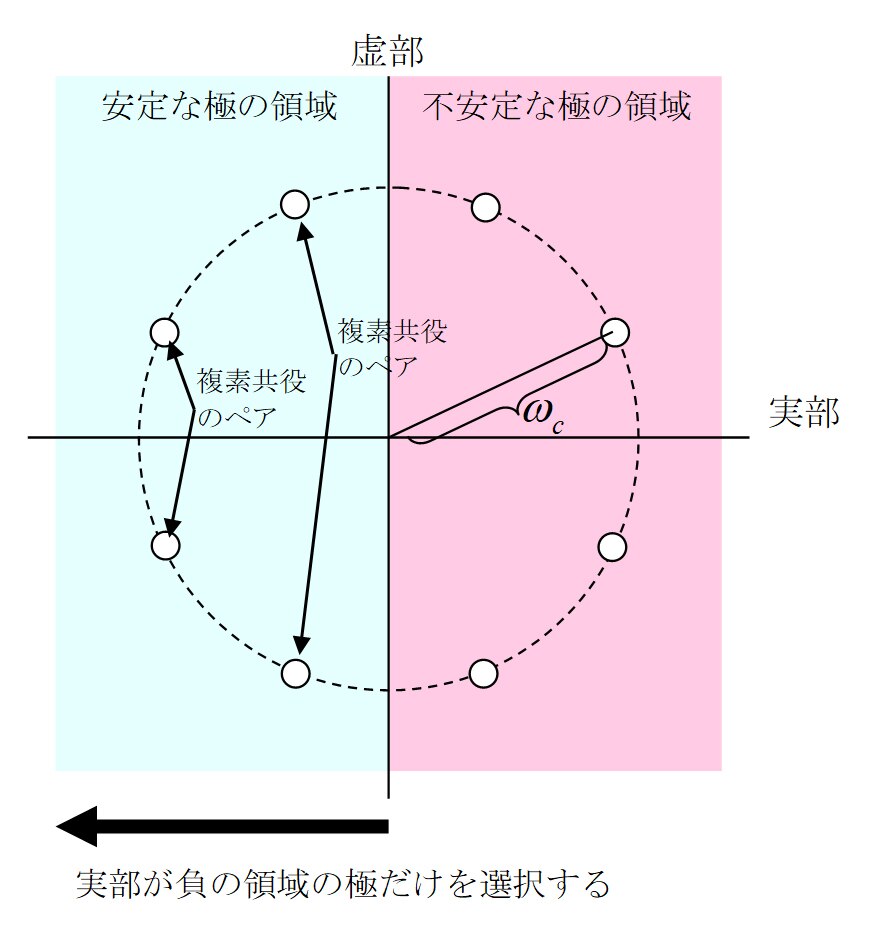
Fig.5 極の選択方法
これらの2 個の極は、Fig.5 に示されるように半径 ωc の円周上に等間隔に並びます。
この中からどのようにして半数のN 個の極を選ぶかについてですが、実は安定したフィルタを実現するためには、左半平面にあるN 個の極だけを選ぶ必要があります。すなわち、実部の符号が負になる極を選べばよいということになります。
*
次回は、極を求めるためのプログラムをMATLAB®とC言語で作成し比較するところから解説します。
※MATLABは、MathWorks社の登録商標です。
関連コラム
Contact
©2025-2026 SOLIZE Ureka Technology Corporation. All rights reserved.